Ａ．アインシュタインの相対論

ヨビノリでアインシュタインの業績について説明していたので、

https://youtu.be/Yjc8R3X1WyA
私もちょっと語りたいと思います。

・

2005年は「世界物理年」と称して、世界各地でさまざまな催しが開催されました。これは「1905年：奇跡の年」の100周年を記念したものです。

・

1905年はスイス特許局に勤めていたアインシュタインが物理学に関する5本の論文を発表した年です。1年間に5本もの論文が学術雑誌に載ること自体も驚異ですが、5本ともノーベル賞級の研究というのも驚きです。
3月「光の生成と変換に関する、ひとつの発見的観点について」
4月「分子の大きさを求める新手法」
5月「熱の分子運動論から要請される、静止液体中に浮かぶ小さな粒子の運動について」
6月「運動物体の電気力学」
9月「物体の慣性は、その物体に含まれるエネルギーに依存するか」

・

アインシュタインは相対性理論で有名ですが、ノーベル賞の対象になったのは光電効果を解明した光量子仮説です。
相対性理論は難しく当時のノーベル賞の選考委員が理解できなかったから、という都市伝説があります。また、当時のドイツの政治情勢が選考対象に影響したという噂もあります。
いずれにせよ、どの研究で受賞してもおかしくないレベルということなのです。

・

超絶有名な相対性理論ですが、相対論には「特殊相対性理論」と「一般相対性理論」の２種類があるのは周知のコトですし、特殊相対性理論という表題の一本の論文があると誤解されているのも相対論アルアルです。
特殊相対性理論は、1905年に発表された「運動する物体の電気力学」とそれを補完する数篇の論文からなる集合体の総称です。
ただ、「運動する物体の電気力学」を特殊相対性理論と呼ぶ人は多いです。

・

ここで変だと気付いた人は鋭いです。

・

電気力学？

・

「運動する物体の時間と空間」では？

・

多くの書籍やウェブサイト、動画での特殊相対性理論の解説は「光速度不変を仮定したとき、時間も空間も観測者との相対的関係において変化する」ことを述べています。

・

この時空の相対性については論文「運動する物体の電気力学」の前半に書かれていて、後半の「マックスウェル方程式がいかなる慣性系でも成立する」ための前提だったのです。

・

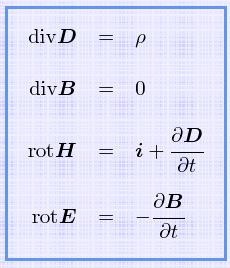
今では前提が主役になっております。

・

また、一般相対性理論も一つの論文ではなく
1911年 「光の伝播に対する重力の影響」
1914年 「一般相対性理論および重力論の草案」
1915年 「水星の近日点の移動に対する一般相対性理論による説明」
1916年 「一般相対性理論の基礎」
1916年 「ハミルトンの原理と一般相対性理論」
1917年 「一般相対性理論についての宇宙論的考察」
1918年 「重力波について」
という論文の集合体なのです。（Wikipediaから抜粋）

・

ただ特殊相対性理論は1905年、一般相対性理論は1915年ということが多いようです。

/

【さて】世界一有名な数式である　E=mc² 　について
Wikipedia：アルベルト・アインシュタインには

「1907年、有名な式E=mc²を発表（1905年9月にm=L/V²の形で既に発表している）。」という一文があります。

1905年9月の論文とは「物体の慣性は、その物体に含まれるエネルギーに依存するか」でした。この論文は日本語訳があります。

/

『光の平面波からなる系が、座標系(x, y, z)から見たときにエネルギーlをもち、光の進行方向（波面に対する法線方向）は、その座標系のx軸と角度φをなすものとしよう。
座標系(x, y, z)に対して等速度で平行移動している、もうひとつの座標系(ξ,η,ζ)を導入し、その原点はx軸に沿って速度vで動いているものとすと、この光の集団のエネルギーは～座標系(ξ,η,ζ)で測定すると～次のようになる』

/

以下『　』内の言葉はアインシュタインの論文の和訳（アインシュタイン論文選「奇跡の年」の５論文：ジョン・スタチェル編、青木薫訳）から抜粋したものです。

/

アインシュタインの論文ではLの小文字ｌを用いているのですが、数字の1と間違えやすいので、ギリシャ文字μを使うことにします。

/

座標系(ｘ,ｙ,ｚ)のエネルギー：μ
座標系(ξ,η,ζ)のエネルギー：μ'

/

これを図示すると次のようになります。

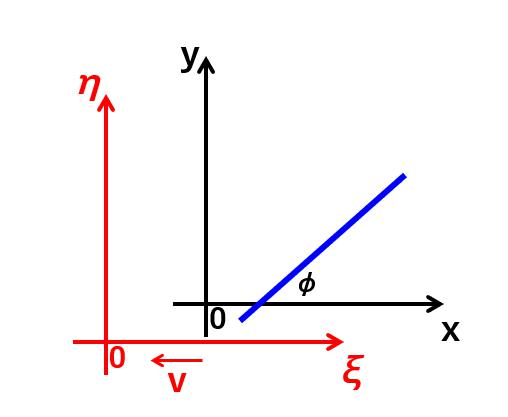
『μ'＝μ*(1－(v/V)*cosφ)/(sqrt(1－(v/V)²))』

かけ算記号「×」は、英小文字「x」と紛らわしいので、以下では「*」記号をかけ算記号として使います。

/

アインシュタインのこの時期の論文には、光速度をVと表記しています。

/

『座標系(x, y, z)で静止している物体があるとき、座標系(x, y, z)で見たときの、その物体のエネルギーをE₀としよう。また同じ物体のエネルギーを、上述のように速度vで運動している座標系(ξ,η,ζ)で測定したものを、Ｈ₀としよう。

/

その物体が、x軸と角度φをなす方向に、エネルギーL/2（座標系(x, y, z)で測定した値）をもつ光の平面波を放出し、同時に、それと同量の光を逆の向きに放出したとしよう。その物体はこの間、座標系(x, y, z)で静止している。』

/

これを図示すると次のようになります。

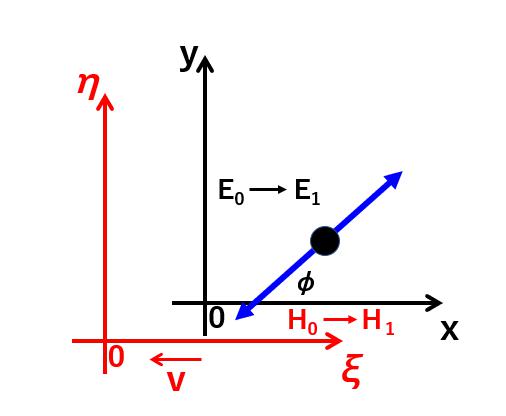
座標系(x, y, z)
E₀＝E₁＋(L/2)＋(L/2)

/

座標系(ξ, η, ζ)
H₀＝H₁
　　＋(L/2)*(1－(v/V)*cosφ)/(sqrt(1－(v/V)²))
　　＋(L/2)*(1＋(v/V)*cosφ)/(sqrt(1－(v/V)²))

/

これらの式の差をとると，

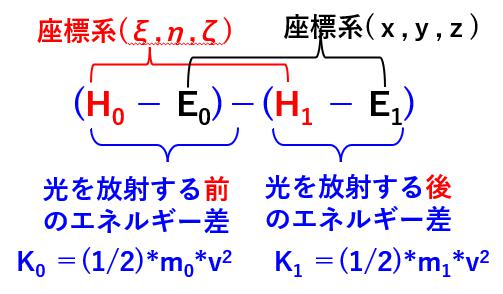
次式が得られます。

/

(H₀－E₀)－(H₁－E₁)
　　＝{(H₁
　　　　＋(L/2)*(1－(v/V)*cosφ)/(sqrt(1－(v/V)²))
　　　　＋(L/2)*(1＋(v/V)*cosφ)/(sqrt(1－(v/V)²))}
　　　　－(E1＋(L/2)＋(L/2))
　　　　－(H1－E1)
　　＝H₁＋L/(sqrt(1－(v/V)²))
　　　　－E₁－L－H₁＋E₁
　　＝L*((1/(sqrt(1－(v/V)²)))－1)

/

『差 H－Eは，付加的な定数Ｃを別にして、他方の座標系(ξ,η,ζ)で見たときの、物体の運動エネルギーKである。Ｃは光が放出される過程で変化することはないから、次のように置いてよい。』

/

『H₀－E₀＝K₀＋Ｃ』
　　＝(1/2)*m₀*v²＋Ｃ
K₀：光の放射前の物体の運動エネルギー
Ｃ：積分定数

/

『H₁－E₁＝K₁＋Ｃ』
　　 ＝(1/2)*m₁*v²＋Ｃ
K₁：光の放射後の物体の運動エネルギー
Ｃ：積分定数

/

したがって

『K₀－K₁　　
　　 ＝L*((1/(sqrt(1－(v/V)²)))－1)』
　　＝(1/2)*(m₀-m₁)*v²
　　＝(1/2)*(Δm)*v²

/

アインシュタインはいきなり
『第４次以上の量は無視すると』
と言って

/

『K₀－K₁＝L*(1/2)*(v/V)²』

/

と書いています。

/

端折りすぎです。理論物理の論文を書く人にとっては当たり前の省略でも、「読み物」としてこの論文を見ているひとにとっては、書いていないと「？」です。

/

K₀－K₁＝L*((1/(sqrt(1－(v/V)²)))－1)

のうちの
((1/(sqrt(1－(v/V)²)))－1)
の部分の(v/V)をxと置いて

/

f(x)＝(1－x²)^(－1/2)－1
としてxについてマクローリン展開します。

7

マクローリン展開とは

「無限回微分可能な関数f(x)は、多項式で近似できる。

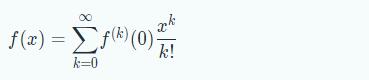
すなわち、右辺は，

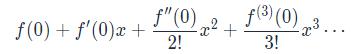
のように展開できる。」ということです。

7

それでは、各項を求めていきましょう。

/

xº の係数は
f(0)/0!＝0

/

x¹ の係数は
f'(x)/1!＝{x*(1－x²)^(－3/2)}/1!
x＝0
→f'(0)/1!＝0

/

x² の係数は
f''(x)/2!＝{(1－x²)^(－3/2)
　　　　　 +3*(x²)*(1－x²)^(－5/2)}/2!
x＝0
→f''(0)/1!＝1/2

/

x³ の係数は
f'''(x)/3!＝{9*x*(1－x²)^(－5/2)
　　　　　　＋15*(x^³)*(1－x²)^(－7/2)}/3!
x＝0
→f'''(0)/3!＝0

/

x⁴ の係数は
f''''(x)/4!＝{9*(1－ x²)^(－5/2)
　　　　　　＋90*( x²)*(1－ x²)^(－7/2)
　　　　　　＋105*(x⁴)*(1－x²)^(－9/2)}/4!
x＝0
→f''''(0)/4!＝9/4!＝3/8

/

以下同様に続きます。

/

したがって

f(x)＝(1/2!)*x²
　　＋(9/4!)*x^⁴
　　＋(225/6!)*x^⁶
　　＋(11025/8!)*x^⁸
　　＋+・・・

/

x を v/V　に戻すと
f(v/V)＝(1/2)*(v/V)²
　　＋(3/8)*(v/V)^⁴
　　＋(5/16)*(v/V)^⁶
　　+(35/128)*(v/V)^⁸
　　+・・・

/

∴K₀－K₁
　＝L*((1/(sqrt(1－(v/V)²)))－1)
　＝L*((1/2)*(v/V)²
　　　＋(3/8)*(v/V)^⁴
　　　＋ (5/16)*(v/V)^⁶
　　　＋(35/128)*(v/V)^⁸
　　　＋・・・)

→４次以降は無視できるほど小さいので無視することとします

/

∴ K₀－K₁＝L*(1/2)*(v/V)²

/

ようやくアインシュタインの述べた『第４次以上の量は無視すると』に辿り着けました。

/

したがって
K₀－K₁＝(1/2)*(m₀-m₁)*v²
　　　＝(1/2)*(Δm)*v²
から
(1/2)*(Δm)*v²＝L*(1/2)*(v/V)²

/

両辺を(1/2)*v²（≠0）で割ると

/

Δm＝L/V²

/

Δmは微量な質量を表しますから、単純に質量mと書くことができます。
今風に、エネルギー：E、光速度：c　とすると、

/

m＝E/c²

/

両辺に　c²　を乗じて

/

E＝m*c²

/

が求められます。

/

ところがアインシュタインは、この　E＝m*c²（アインシュタイン論文での書き方に従えば　L＝m*V²）を書かず、

/

『K₀－K₁＝L*(1/2)*(v/V) ²

を得る。
この方程式から、ただちに次の結論が得られる。
物体が、エネルギーLを放射の形で放出すると、その物体の質量は、L/V ² だけ減少する。』
と（控えめに？）述べていますが・・・

・

では、1905年にすでに発表しているにもかかわらず、1907年にE＝m*c² の論文を発表したとはどういうことなのでしょうか？

/

Wikipedia：アインシュタインの原論文
物理学者アルベルト・アインシュタインの著した原論文のうちPDFファイルの形式でWeb上での閲覧が可能なものを年代順に羅列している。

/

によれば、

/

A. Einstein (1905-09-27). “Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? [物体の慣性はそのエネルギーの大きさに依存するか]”

の原論文はドイツ語で3ページ、、

/

一方

/

A. Einstein (1907-05-14). “Über die vom Relativätsprinzip geforderte Trägheit der Energie” [邦訳は無いようです]

の原論文はドイツ語で14ページです。

/

ドイツ語読めないので、中身を語ることはできませんが、
1907年の論文の結論めいた式が
ε＝μ*(V²)*(1/sqrt(1－(v/V)²）
ここで　εはエネルギー、μは質量、Vは光速度、vは物体の移動速度です。
物体が静止しているとき　v＝0　なので、
ε＝μ*V²

/

現代の表記にすると
E＝m*c²
です。

/

理論物理の論文の一般的な傾向なのかもしれませんが、アインシュタインの論文は説明のための図表がほとんどありません。
読めないドイツ語の中に点在する数式を眺めてみても、想像がつきません。

/

推測するに、1905年の議論をより深めて確信を得たのが1907年の論文、といえるのではないのかと。

/

一方、一般相対性理論にとって1907年は画期的な年で、「等価原理」の着想を得た年でもあるのです。

/

「運動する物体の時間と空間」を学ぼう
ヨビノリ：中学数学からはじめる相対性理論

https://youtu.be/voFHToRM4xI

・

/